Spin-Resolved Topology and Partial Axion Angles in Three-Dimensional Insulators

Kuan-Sen Lin, Giandomenico Palumbo, Zhaopeng Guo, Yoonseok Hwang, Jeremy Blackburn, Daniel P. Shoemaker, Fahad Mahmood, Zhijun Wang, Gregory A. Fiete, Benjamin J. Wieder, Barry Bradlyn
January 2024
Cite Journal ArXiv Laser Focus World Research Highlight Physics World Research Highlight Press Release IPhT News Coverage

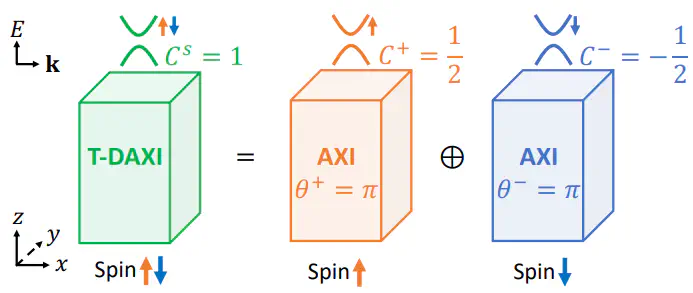
Abstract

Symmetry-protected topological crystalline insulators (TCIs) have primarily been characterized by their gapless boundary states. However, in time-reversal- (T-) invariant (helical) 3D TCIs—termed higher-order TCIs (HOTIs)—the boundary signatures can manifest as a sample-dependent network of 1D hinge states. We here introduce nested spin-resolved Wilson loops and layer constructions as tools to characterize the intrinsic bulk topological properties of spinful 3D insulators. We discover that helical HOTIs realize one of three spin-resolved phases with distinct responses that are quantitatively robust to large deformations of the bulk spin-orbital texture: 3D quantum spin Hall insulators (QSHIs), “spin-Weyl” semimetals, and T-doubled axion insulator (T-DAXI) states with nontrivial partial axion angles indicative of a 3D spin-magnetoelectric bulk response and half-quantized 2D TI surface states originating from a partial parity anomaly. Using ab-initio calculations, we demonstrate that β-MoTe2 realizes a spin-Weyl state and that α-BiBr hosts both 3D QSHI and T-DAXI regimes.

Publication
Nature Communications 15, 550. See below for a seminar given at the PCS Institute for Basic Science in Daejeon, South Korea in 2022.

Experimental Note: Experimental support for our prediction of 3D ``Ising-like’’ SOC in α-BiBr provided in Nature Communications 14, 8089 (2023).

Code Note: The nested and spin-resolved Wilson loop code for this work, along with example scripts and documentation, have been made freely available as User-Contributed Resources for the open-source Rutgers Python Tight-Binding (PythTB) Python package.