Wallpaper fermions and the nonsymmorphic Dirac insulator

Abstract

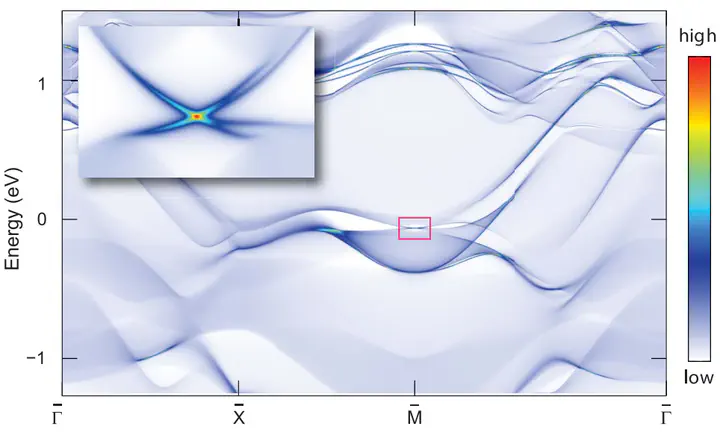
Materials whose gapless surface states are protected by crystal symmetries include mirror topological crystalline insulators and nonsymmorphic hourglass insulators. There exists only a very limited set of possible surface crystal symmetries, captured by the 17 “wallpaper groups.” Here we show that a consideration of symmetry-allowed band degeneracies in the wallpaper groups can be used to understand previously described topological crystalline insulators and to predict phenomenologically distinct examples. In particular, the two wallpaper groups with multiple glide lines, pgg and p4g, allow for a topological insulating phase whose surface spectrum consists of only a single, fourfold-degenerate, true Dirac fermion, representing an exception to a symmetry-enhanced fermion-doubling theorem. We theoretically predict the presence of this phase in Sr₂Pb₃ in space group 127 (P4/mbm).