Abstract
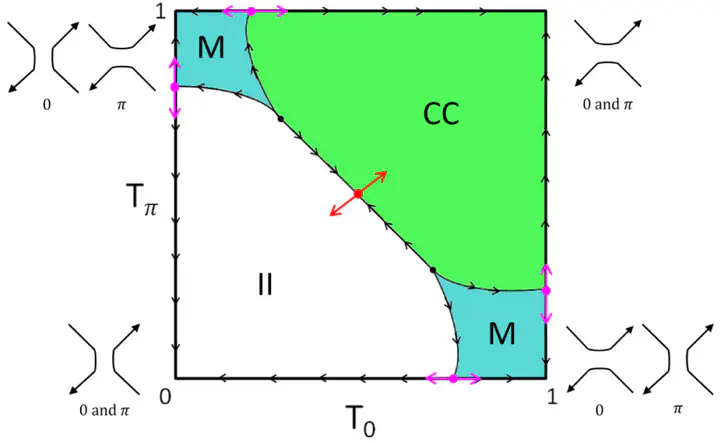
Bilayer graphene in a perpendicular electric field can host domain walls between regions of reversed field direction or interlayer stacking. The gapless modes propagating along these domain walls, while not strictly topological, nevertheless have interesting physical properties, including valley-momentum locking. A junction where two domain walls intersect forms the analog of a quantum point contact. We study theoretically the critical behavior of this junction near the pinch-off transition, which is controlled by two separate classes of nontrivial quantum critical points. For strong interactions, the junction can host phases of unique charge and valley conductances. For weaker interactions, the low-temperature charge conductance can undergo one of two possible quantum phase transitions, each characterized by a specific critical exponent and a collapse to a universal scaling function, which we compute.